Aufgabe A 1.1
Der Graph der Funktion f mit f(x)=-0,1x3+0,5x2+3,6 beschreibt modellhaft für -1≤x≤5
das Profil eines Geländequerschnitts.
Die positive x-Achse weist nach Osten, f(x) gibt die Höhe über dem Meeresspiegel an
(1 Längeneinheit entspricht 100 m).
a) Auf welcher Höhe liegt der höchste Punkt des Profils?
In dem Tal westlich dieses Punktes befindet sich ein See, der im Geländequerschnitt an
seiner tiefsten Stelle 10 m tief ist.
Bestimmen Sie die Breite des Sees im Geländequerschnitt.
Ab einer Hangneigung von 30° besteht die Gefahr, dass sich Lawinen lösen.
Besteht an der steilsten Stelle des Profils zwischen See und höchstem Punkt Lawinengefahr?
(5 VP)
b) Am Hang zwischen dem höchsten Punkt und dem westlichdavon gelegenen Tal befindet sich ein
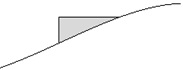in den Hang gebautes Gebäude, dessen rechteckige
Seitenwand im Geländequerschnitt liegt.
Die Abbildung zeigt den sichtbaren Teil dieser
Seitenwand. Die Oberkante der Wand verläuft
waagrecht auf 540 m Höhe.
Von dieser Kante sind 28 m sichtbar.
Untersuchen Sie, ob der Flächeninhalt des sichtbaren Wandteils größer als
130 m² ist.
(3 VP)
c) Der zweite Verlauf des Profils nach Osten hin kann durch eine Parabel zweiter Ordnung modelliert werden, die sich ohne Knick an den Graphen von f anschließt. Ihr Scheitel liegt bei x=6 und beschreibt den tiefsten Punkt eines benachbarten Tals.Auf welcher Höhe befindet sich dieser Punkt?
(4 VP)
Aufgabe A 1.2
Gegeben ist die Funktion h mit
,
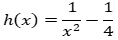deren Graph symmetrisch zur y-Achse ist.
Es gibt einen Kreis, der den Graphen von h in dessen Schnittpunkten mit der x-Achse berührt.Berechnen Sie die Koordinaten des Mittelpunktes dieses Kreises.
(3 VP)